فيديو توضيح قسمة عدد كسري

حل المعادلة التربيعية باستخدام المميز

مميز المعادلة التربيعية :
 

الأهداف :
 عزيزي الدارس يتوقع منك بعد دراسة هذا الدرس أن تكون قادراً على التعرف على مميز المعادلة التربيعية واستخدام المميز في معرفة نوع المعادلة إن كانت تحلل أو لا.

 

تمهيد :
 هل يمكن إيجاد جذور لجميع المعادلات التربيعية ؟

ـ ما جذور المعادلة س² + س + 12 = صفر  ؟

ـ ما جذور المعادلة س² + 1 = صفر  ؟

لو بحثت في إيجاد حل للمعادلتين السابقتين أي إيجاد جذور كل منهما فلن تجد لهما حلاً .

أي ليست كل المعادلات التربيعية يمكن حلها .
 

والسؤال الآن : كيف يمكن أن نميز بين المعادلات التربيعية التي يمكن حلها والتي لا حل لها ؟

الجواب : هو استخدام المميز ( ب² 4 أ جـ) حيث ب هو معامل س ، أ هو معامل س² ، جـ الحد المطلق .

إن مميز المعادلة التربيعية ( ب² 4أ جـ ) هو الذي يحدد إذا كان للمعادلة جذور ( لها حل ) أو لا جذور لها ( ليس لها حل ) حيث إذا كان المميز أكبر من الصفر ( موجب ) أو يساوي صفراً فإن المعادلة لها حل .أما إذا كان أقل من الصفر فإن المعادلة ليس لها حل .

وبالرموز :

ب² 4 أ جـ ≤  صفر لها حل .

ب² 4 أ جـ < صفر ليس لها حل .

نظرية فيتاغوس

نص هذه النظرية " في المثلث القائم الزاوية مربع طول الوتر يساوي مجموع مربعي طولي الضلعين الاخرين في المثلث "

   ABC مثلث قائم الزاوية في A  وهذا يعني أن الوتر هو القطعة المستقيمة [ BC ] المقابلة للزاوية القائمة ومنها نستنتج أن :

 

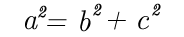
عكس نظرية فيثاغورث "إذا كان مربع طول ضلع مثلث يساوي مجموع مربعي طولي الضلعين الآخرين فان المثلث يكون قائم الزاوية "