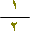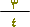تحويل الكسر العادي إلى كسرٍ عشري الأهداف :ـ  أن يتقن الدارس عملية تحويل الكسور العادية إلى كسور عشرية .  الخبرات السابقة : ـ الكسور والأعداد الكسرية ، الكسور العشرية ، عمليات القسمة الطويلة ، مفهوم الضرب في الواحد الصحيح . الإجراءات والأنشطة : أ. تعلمت سابقاً أن الكسور العادية التي يكون مقامها 10 ، 100 ، 1000 … الخ ، يمكن تحويلها بسهولة إلى كسر عشري ، ذلك لأن هذه الكسور هي أعشار أو أجزاء من مئة أو أجزاء من ألف … ، وتكون أجزاؤها العادية كأجزاء الكسور العشرية . ب. الكسور العادية التي مقاماتها ليست العشرة أو مضاعفاتها (قواها) .  1) يُمكن تحويل الكسور العادية إلى كسور عشرية وذلك بضرب كل من البسط والمقام في العدد الذي يجعل مقام الكسر العادي العشرة أو مضاعفاتها  10 ، 100 ، 1000 ... وهكذا . إلى كسر عشري . مثال (1) : حوِّل الكسر    الحل : إلى كسر عشري . مثال (2) : حوِّل الكسر     الحل :

ما هو الكسر العشري ، وما علاقته بالكسر العادي ؟ تمهيد :  نقول أن الكسر العشري حالة من حالات الكسر العادي مقامه العشرة أو مضاعفاتها (10 ، 100 ، ... )  وتُستعمل في الكسر العشري الفاصلة العشرية ( , ) بدل خط الكسر ، وسميت كذلك لأنها تفصل بين الأعداد الصحيحة والأجزاء العشرية . 2) عرفت سابقاً أن العدد 76.583 مكون من 7 عشرات صحيحة أي   70 لاحظ هنا أن الوحدة المميزة مقسومة في الكسر العشري إلى 10 أقسام متساوية أو 100 من الأقسام المتساوية أو  1000 من الأقسام المتساوية ... الخ .  ويبين الكسر العشري عدد الأقسام الموجودة في كل فئة .

احتمال عدم ظهور الحادث

الهدف : أن يتعرف الدارس إلى مفهوم احتمال عدم ظهور الحادث وعلاقته باحتمال ظهور الحادث نفسه .
الإجراءات والأنشطة :

أ) لنبدأ هنا بتجربة رمي قطعة معدنية مرة واحدة  :   = { وجه , خلف }

احتمال ظهور وجه =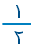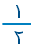 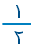         ,     احتمال ظهور خلف =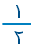 

احتمال الحادث الأكيد = احتمال ظهور ( وجه أو خلف ) = احتمال ( ظهور وجه ) + احتمال ( ظهور خلف )
                                                                   =             +          

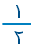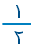
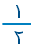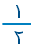
                                                            =   1 واحد صحيح

   

إذا سألتَ نفسك : ما احتمال "عدم ظهور وجه "عند رمي قطعة معدنية لمرة واحدة ... ماذا تعني بذلك ؟؟  

هل تتفق معي أن هذا يعني احتمال "ظهور خلف" !!

وبالمثل : احتمال عدم ظهور خلف يعني في هذه  التجربة احتمال "ظهور وجه" .

ب)  في تجربة سحب كرة من ثلاث كرات :  = {كرة حمراء , كرة صفراء , كرة خضراء }ـ ما احتمال "سحب كرة غير الكرة الحمراء" ؟؟ هذا يعني احتمال ... !!       "سحب كرة خضراء أو كرة صفراء"  ـ وما احتمال "سحب كرة غير الكرة الخضراء "هذا يعني احتمال ...     "سحب كرة صفراء أو كرة حمراء"

 وماذا إذا قلنا :  ما احتمال "سحب كرة غير الخضراء وغير الصفراء" !!

نحن بالضبط نعني هنا ,  مااحتمال "سحب كرة حمراء" !!

احتمال وقوع الحادث

الهدف : أن يتعرف الدارس كيفية تحديد احتمالات وقوع الحادث .

الإجراءات والأنشطة :

 أولاً :

في تجربة رمي حجر النرد مرة واحدة ، يُمكننا أن نحصل على العدد (5) ونُسمي هذا : حادث "الحصول على العدد 5" .

نَحنُ نعرف ان هنالك "6" نواتج ممكنة ، هي عناصر الفضاء العيني لتجربة رمي حجر النرد مرة واحدة . 

ونعرف أنّ أي ناتج من هذه النواتج له فرصة الحدوث نفسها بمعنى : فرصة ظهور الرقم 5 هي نفس فرصة ظهور الرقم 6 ونفس فرصة ظهور الرقم 2 ....  

نقول أن احتمال وقوع حادث "الحصول على العدد 5 " هو 1 من 6 ويُكتب على الصورة .

ل ( ح ) =

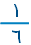لاحظ هنا أن احتمال وقوع حادث "الحصول على الرقم (5) هو حادث بسيط "

  ح = {5}   مجموعة جزئية تحتوي على عنصرٍ واحد وهو حادث له فرصة ظهور تساوي فرصة ظهور أي حادث بسيط آخر في هذه التجربة :

ح3 = {3}	,	ح2 = {2}	,	ح1 = {1}
ح6 = {6}	,	ح5 = {5}	,	ح4 ={4}

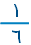ل (ح1) = ل(ح2) = ل(ح3) = ل(ح4) = ل(ح5) = ل(ح6) =

ثانياً : 
في تجربة رمي حجر  النرد مرة واحدة ، يُمكننا أيضاً أن نحصل على الرقم 5 أو الرقم 6 . نُسمي هذا
"حادث الحصول على رقم أكبر من الرقم 4 ".

 ح₁ = {5 , 6}

نحنُ نعرف أن هنالك (6) نواتج ممكنة هي عناصر  الفضاء العيني لتجربة رمي حجر  النرد مرة واحدة .
نقول أن احتمال وقوع حادث " الحصول على رقم أكبر من الرقم 4 " هو 2 من 6 .

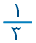أي

ويُكتب ل (ح1) =

مفهوم الاحتمال ( الفرصة )

الهدف : أن يتعرف الدارس إلى مفهوم الاحتمال (الفرصة) .
 

الإجراءات والأنشطة :

في تجربة رمي حجر نردٍ مرة واحدة ، تبين لك أن هنالك ستة (6) نواتج ممكنة . 

وفي تجربة رمي قطعة نقدٍ معدنية مرة واحدة ، تبين  لك أن الفضاء العيني هو مجموعة النواتج الممكنة

} خلف ، وجه {           أو نقول                } صورة ،   كتابة {

ـ ولكن ماذا عن احتمال (فرصة) ظهور وجه عند رمي قطعة النقد مرة واحدة ؟

ـ وماذا عن احتمال (فرصة) ظهور الرقم (6) عند رمي حجر النرد مرة واحدة ؟؟

لاحظ هنا أن وجهي قطعة النقد متماثلين ولا يختلفان إلا في التسمية ، ولاحظ ان أوجه حجر النرد أيضاً متماثلة ( حجر النرد هو معكعب متماثل تماماً ) .

إذا درسنا تجرية رمي حجر النرد ، نستطيع بسبب هذا التماثل أن نقول بأن فرصة ظهور الرقم 1 إلى أعلى تساوي فرصة ظهور الرقم 2 وتساوي فرصة طهور الرقم 3 ...... وهكذا .

 هذا يعني أن النواتج الممكنة لها نفس فُرصة الظهور .

ـ احتمال (فرصة) ظهور وجه عند رمي قطعة النقد مرة واحدة يساوي     ؟

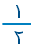ـ واحتمال ( فرصة ) ظهور الرقم (6) عند رمي قطعة النرد مرة واحدة يساوي    ؟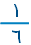
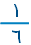حسناً.....

ـ كم عَددِ عناصر الفضاء العيني لتجربة رمي قطعة النرد مرة واحدة ؟؟

     ستة (6)  عناصر مميزة    { 1 ، 2 ، 3 ، 4 ، 5 ، 6 } 
 

ـ وكم عدد مرات ظهور الرقم (6) في النواتج الممكنة لتجربة رمي قطعة النرد مرة واحدة ?

  مرّة واحدة

ـ احتمال ( فرصة ) ظهور الرقم( 6 ) = 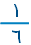      وبالمثل فإن فرصة ظهور الرقم 2 =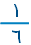  
                                                                                والرقم 5 = 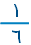      ......... وهكذا
                                                                               

لاحظ  هنا  أن كل ناتج ممكن  في هذه التجربة له نفس فرصة الظهور .
نقول  :
	فرصة ظهور ناتج ما =

                       

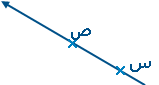
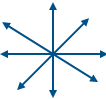
أولاً : أدرس المجموعات التالية : أ  = مجموعة مضاعفات العدد 5 . ب = مجموعة الكسور . = مجموعة نقاط الشعاع ن مجموعة المستقيمات التي تمر بالنقطة م هل تستطيع حصر عدد مضاعفات العدد 5 ؟ وهل تستطيع حصر عدد المستقيمات التي تمر بالنقطة م ؟ ماذا تلاحظ ؟؟ يستحيل تحديد عدد عناصر أي من المجموعات هذه .   نُسمي المجموعة التي لا يُمكن تحديد ( تعيين ) عدد عناصرها مجموعة غيرُ منتهية 1) ص = { 1 , 3 , 5 , ...... } نقول عن المجموعة ص أنها مجموعة محصورة من الأسفل . ص = أ : أ  الأعداد الفردية  £ 1 لاحظ هنا أن المجموعة ص غير محصورة من أعلى . 2) ع = { 2 , 1 , 0 , ـ1 , ـ 2 , ........ } نقول عن المجموعة ع أنها مجموعة محصورة من الأعلى . ونلاحظ أنها غير محصورة من أسفل .

المجموعة الجزئية
 

الهدف : أن يتعرف الدارس إلى مفهوم المجموعة الجزئية وعلاقتها بالمجموعة الرئيسة .

الاجراءات والأنشطة :

لنأخذ المجموعة س التي تمثل أرقام العدد 8624

س = { 4 , 2 , 6 , 8 }

 يمكننا تكوين مجموعة أو مجموعات جزئية من هذه المجموعة الرئيسة بأخذ عنصر أو أكثر منها وكتابتها ضمن مجموعة جديدة .
 

ع = { 6 , 8 , 2}	ص = { 4 }
د =  { 6 , 2 , 4 }   ... وهكذا	ل = {4 , 6 }

 ماذا تُلاحظ هنا : كل عناصر ع تنتمي إلى س 

                        كل عناصر ل  تنتمي إلى س

                        كل عناصر د تنتمي إلى  س

                        كل عناصر ص تنتمي إلى س

  
نقول هنا:  ع  مجموعة جزئية من  س  أو نقول  ع  محتواة في  س

                 نعبر عن هذه الجمل بالصورة الرياضية التالية ع ة س
 

 نقول: ل  محتواة في س

ل  ة  ...  تُقرأ         ل محتواه في ...

ل  ة س

                                أو   ل مجموعة جزئية من .....

  ونقول: المجموعة ص مجموعة جزئية من المجموعة الكلية س

ص  ة  ...  تُقرأ       ص محتواة في .......

ص  ة  س

                                                  أو   ص مجموعة جزئية من .....
 

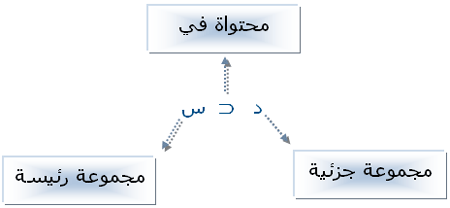كتابة المجموعة بذكر الصفة المميزة

الهدف : أن يتعرف الدارس إلى كيفية الكتابة الرياضية لمجموعة ما بذكر الصفة المميزة  لعناصرها.

الإجراءات والأنشطة :

 أولاً :    

الصفة المميزة		المجموعة
كل عنصر هو فصل من فصول السنة		س = } الصيف ، الربيع ، الشتاء ، الخريف {	1.
كل عنصر هو عدد زوجي يقع بين  1 ، 9		ع = {  2  ، 4  ، 6 ،   8 }	2.
كل عنصر هو عدد فردي يقع بين 10 ، 20		ل = {  11 ، 13 ، 15 ، 17 ، 19 }	3.
كل عنصر هو يوم من أيام الأسبوع	و = } السبت ، الأحد ، الاثنين ، الثلاثاء ، الاربعاء ، الخميس والجمعة{		4.

    
يمكننا التعبير عن مجموعة ما ، بكتابة الصفة المميزة بدلاً من ذكر وكتابة عناصرها

مثل1 :

 المجموعة الأولى = } س : س فصل من فصول السنة {

وتُقرأ مجموعة فصول السنة ( س ) حيث س فصل من فصول السنة .

المجموعة الثانية = } ع : ع عدد زوجي يقع بين 1 ، 9 {

وتُقرأ مجموعة الأعداد الزوجية ( ع ) ، حيث ع عدد زوجي يقع بين 1 ، 9 .

المجموعة الثالثة : ص = } ل : ل عدد فردي يقع بين 10 ، 20 {

وتُقرأ ص مجموعة الأعداد الفردية ( ل ) حيث ل عدد فردي يقع بين 10 ، 20 .

المجموعة الرابعة : س = } و : و يوم من أيام الأسبوع {

وتقرأ س مجموعة أيام الاسبوع ( و ) حيث و  يوم من أيام الأسبوع .

كتابة المجموعة بذكر عناصرها  الهدف :  أن يتعرف الدارس إلى كيفية الكتابة الرياضية لمجموعةٍ ما بذكر عناصرها . الخبرات السابقة : مفهوم المجموعة , العنصر , إنتماء أو عدم إنتماء العنصر إلى مجموعة ما  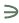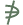( ,)   تمهيد : 1) نستخدم اشارة الحاصرتين {   }  لكتابة عناصر مجموعة ما داخلهما . مثل : مجموعة الفصول الأربعة هي : الصيف ، الشتاء ، الربيع ، الخريف وبالتالي نكتب مجموعة الفصول الأربعة = } الصيف ، الشتاء ، الربيع ، الخريف { 2) عندما نكتب عناصر مجموعة ما داخل اشارة الحاصرتين {     }  لاحظ أننا نصنع الفاصلة ( ، )       بين كل عنصرٍ وآخر .  مجموعة الأعداد الزوجية المحصورة بين العدد (1) و العدد (11) = { 2 , 4 , 6 , 8 , 10} 3) إذا كانت س هي مجموعة الفقاريات التي تضم : (الأسماك ، الزواحف ، الطيور ، البرمائيات ، الثدييات ) فإننا نستطيع التعبير رياضياً عن هذه المجموعة كالتالي  س = } الأسماك ، الزواحف ، الطيور ، البرمائيات ، الثدييات { وكذلك س = } الثدييات ، الطيور ، البرمائيات ، الزواحف ، الأسماك {  وكذلك س = } الزواحف ، البرمائيات ، الثدييات ، الأسماك ، الطيور {